Beispiele aus unserer Forschung
Dynamische Strukturen des Lebens
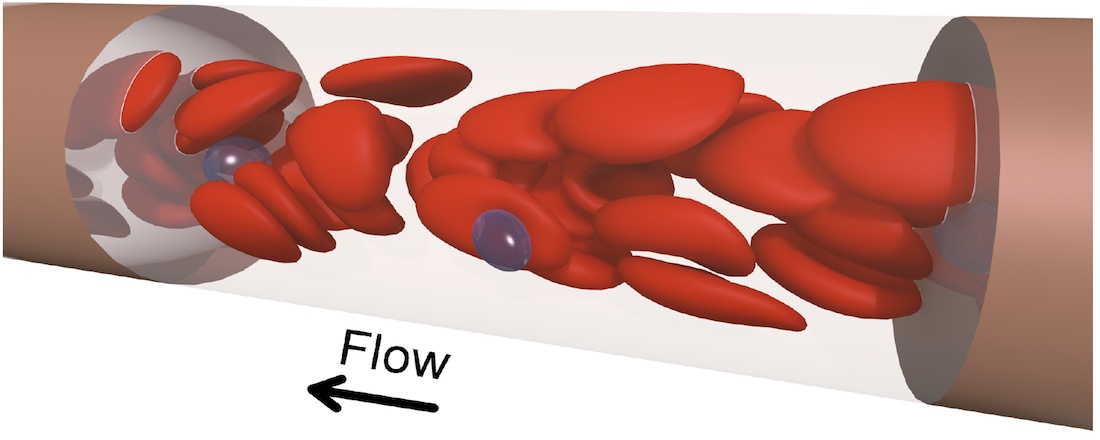
Lebende Systeme bilden räumlich komplexe Strukturen. Die Entstehung von Organismen aus Eizellen (Weiss), das Umhüllen von Fremdkörpern durch Zellmembranen (Kress), das Strömungsverhalten von roten Blutkörperchen (Gekle), die Motilität und Selbstorganisation mikrobieller Gemeinschaften (Bäumchen) oder die Biogeografie (Beierkuhnlein) und Biodiversität (Jentsch) sind nur einige Beispiele. In einer linearen Welt wäre dies nicht möglich. Nichtlinearitäten sind die Voraussetzung für Leben.
Turbulenz
Turbulente Strömungen sind allgegenwärtig in unserem Alltag, sie beeinflussen sowohl das aktuelle Wettergeschehen (Thomas) als auch das Klima (Aizinger). Doch nicht nur hier, auch für eine mögliche zukünftige Energieversorgung aus Windenergie und Fusionsreaktoren oder in der Astrophysik ist ein Verständnis von Turbulenzen (Peeters) essentiell. Die Kombination von Simulationen und statistischer Theorie (Wilczek) ermöglicht neue Ansätze für ein besseres Verständnis dieses komplexen Phänomens.
Netzwerke und künstliche Intelligenz
Durch die Vernetzung einer Vielzahl einfacher, selbstständiger Einheiten entstehen Systeme mit gänzlich neuen Eigenschaften und komplexem, nichtlinearem Verhalten. Dies gilt für Netzwerke magnetischer Partikel (Fischer) oder einzelner Moleküle (Weber) genauso wie für Polymernetzwerke (W. Köhler) und aktiv schwimmende Teilchen (Schmidt). Komplexe Netzwerke sind darüber hinaus ein wichtiger Bestandteil von sozio-ökonomischen Systemen wie Infektionsmodellen (Chudej) oder Supply-Chains (Rambau). Neuronale Netzwerke, wie sie im Gehirn von Tieren vorkommen (Schuster), bilden die Basis für künstliche Intelligenz u.a. in der computergestützten Medizin (Schiela).
Nichtlineare Dynamik der Quantenwelt
Auf kleinsten Skalen verhält sich die Natur oft völlig anders als es die menschliche Intuition erwartet. Die Erforschung dynamischer Phänomene der Quantenmechanik ist essentieller Baustein zum Verständnis von Photosynthese (Kümmel, J. Köhler) oder Halbleitern (Axt). Viele nichtlineare Effekte in der Quantenwelt lassen sich mit Hilfe der random-matrix-Theorie (Kriecherbauer) beschreiben.
Musterbildung und Mustererkennung
Individuen und Ereignisse bilden biopsychosoziale bzw. zeitliche Muster, die mit Hilfe nichtlinearer Methoden erkannt und klassifiziert werden können. Solche Mustererkennungen treten in Vegetationslandschaften (Zimmermann), in der Talentidentifikation im Sport (Hohmann), in geologischen Prozessen (Keppler) oder in mathematischen Systemen wie den Einstein-Vlasov-Gleichungen (Rein) auf. Auf der Basis linearer Methoden alleine wären solche Klassifikationen kaum erfolgreich.
Technologische Anwendungen
Nichtlinearitäten spielen nicht nur in den Naturwissenschaften, sondern auch in technischen Anwendungen eine zentrale Rolle. Beispiele, die an unserer Universität erforscht werden, sind Energiesysteme (Brüggemann) oder Hochdruckmaterialien (Dubrovinskaia). Um Lösungen für solche nichtlinearen Systeme zu finden, benötigt man effiziente Rechenverfahren (Rauber), optimale Steuerungsmethoden (Grüne) sowie ein Verständnis der darin enthalten Unsicherheiten (Bebendorf).
